Leetcode 110 Balanced Binary Tree

Soru

Given a binary tree, determine if it is height-balanced.

For this problem, a height-balanced binary tree is defined as:

a binary tree in which the left and right subtrees of every node differ in height by no more than 1.

Örnek 1

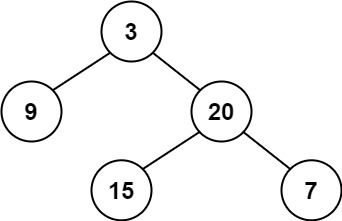
Input: root = [3,9,20,null,null,15,7]
Output: true

Örnek 2

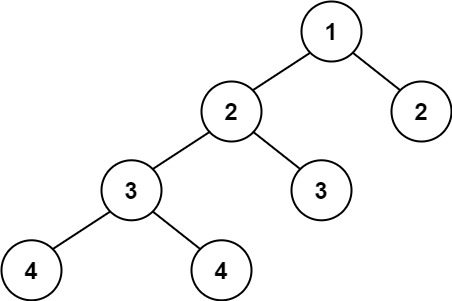
Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

Örnek 3

Input: root = []
Output: true

Çözüm

• LeetCode 110. Balanced Binary Tree sorusunu biliyorum! Bu problem, bir ikili ağacın dengeli (balanced) olup olmadığını belirlememizi istiyor.
• Girdi: Bir ikili ağacın kök düğümü (root).
• Çıktı: Eğer ağaç dengeli ise True, değilse False döndür.
• Bir ikili ağaç şu koşulu sağlıyorsa dengeli (balanced) kabul edilir: Her düğüm için sol ve sağ alt ağaçların maksimum derinlik farkı en fazla 1 olmalıdır.
• Bu soruyu DFS (derinlik öncelikli arama) kullanarak çözebiliriz.Her düğüm için sol ve sağ alt ağaçların derinliğini hesaplarız ve farkı kontrol ederiz.
• Çözüm Açıklaması
• DFS kullanarak her düğüm için derinlik hesaplanır.
• Alt ağaçlardan biri dengesizse, -1 döndürülerek yukarıya iletilir.
• Her düğümde sol ve sağ derinlik farkı hesaplanır.
• Eğer |left - right| > 1 ise dengesizdir ve -1 döndürülür.
• DFS çağrısı bittiğinde, -1 döndürülmemişse ağaç dengelidir.

Code

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        def dfs(node):
            if not node:
                return 0
            
            left = dfs(node.left)
            right = dfs(node.right)

            # Eğer bir alt ağaç dengesizse, -1 döndürerek dengesizliği yukarı ilet
            if left == -1 or right == -1 or abs(left - right) > 1:
                return -1
            
            return max(left, right) + 1
        
        return dfs(root) != -1

Complexity

• Time complexity (Zaman Karmaşıklığı) : O(n) → Her düğüm bir kez ziyaret edilir.
• Space complexity (Alan Karmaşıklığı):
  • Dengeli ağaçta O(log n) → Özyineleme derinliği ağacın yüksekliği kadardır.
  • Dengesiz ağaçta O(n) → Kötü durumda (tek taraflı ağaç) derinlik n olabilir.